 What is the origin of the air we breathe, of the water in our seas and oceans, where does daylight come from, why is there a terrestrial climate, why are there auroras, why...? The answer lies in the sky. The stars are a great supplier of chemical elements, and our Sun is the source of life. Since time immemorial, man has been concerned with knowing more and more about the stars, their movement, their size, their composition... Thus, astronomy was born informing us about the celestial stars. These are described by various characteristics, mass, diameter, rotation, temperature, chemical composition, etc... to which are added the place of this body in the universe, its history, and even, in the case of the sun, its repercussions on the history of humanity.
What is the origin of the air we breathe, of the water in our seas and oceans, where does daylight come from, why is there a terrestrial climate, why are there auroras, why...? The answer lies in the sky. The stars are a great supplier of chemical elements, and our Sun is the source of life. Since time immemorial, man has been concerned with knowing more and more about the stars, their movement, their size, their composition... Thus, astronomy was born informing us about the celestial stars. These are described by various characteristics, mass, diameter, rotation, temperature, chemical composition, etc... to which are added the place of this body in the universe, its history, and even, in the case of the sun, its repercussions on the history of humanity.
Encyclopedias give the latest measurements of our star; their values are consensus, as validated by the International Astronomical Union (IAU). Thus, resolution B3 voted at the IAU GA on August 13, 2015, recommends adopting nominal values for the diameter, luminosity, temperature, and mass of the Sun. But there are other useful parameters to develop solar astrophysics, i.e., to explain poorly understood phenomena, such as the cyclicity of spots, which originate and disappear on a scale of about eleven years.
Among these parameters, one is still almost unknown and has a name rather difficult to understand at first sight, as it would be for the notion of volume, much more accessible. They are the so-called « solar gravitational moments », which may appear, even to specialists, as « strangeness ». Let's try to demystify. A rotating body flattens at the poles. More generally, it deforms. The deformation will depend on two conditions, the speed of rotation (the faster the body rotates, the flatter it becomes) and the internal composition. It is easy to understand that if the body is rigid, like a spherical ball made of steel, its deformation (and thus its flattening) will be very slight. But if the body has a heterogeneous composition, for example a dense core, enveloped by one or more less dense strata not uniformly distributed around the core, the general deformation on the surface will show more or less significant departures from an ideal sphere. To put it simply, a body which is not homogeneous from the center to the surface, and which rotates at different speeds from the equator to the poles, including the interior, will take on a complex external shape, very « dented ». It is these surface distortions that the gravitational moments Jn measure (see Figure 1).
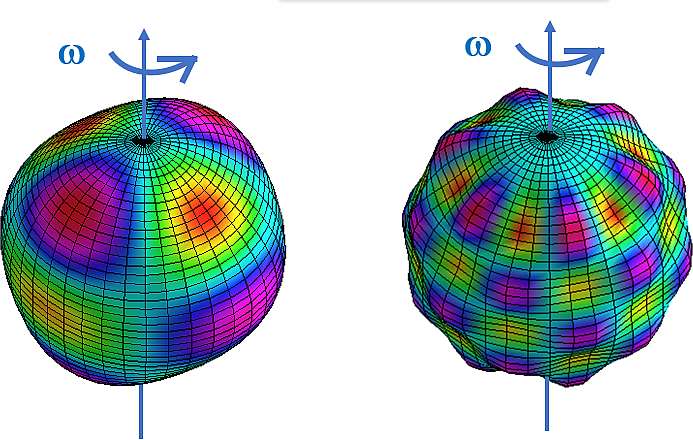
But why are the surface distortions called by this rather barbaric term, gravitational moments ? To understand, in the case of a rotating star, a small volume of mass (m) at its surface, or inside, undergoes two forces. One is due to the gravitational attraction of this star (as if the totality of its mass was concentrated in its center) with other bodies, close or very massive, such as the moon, the sun, the planets... and the other one, a force whose origin is its own rotation. The sum of these two forces is called « gravity ». And « moment » because in physics, the moment of a force translates the ability for this force to drive the system to rotate. We therefore use the term gravitational moment to express the fact that the successive « bumps » are due to gravitation and rotation. The gravitational moment of order 1, called J1, will translate a final figure in the shape of a « pear », while that of order 2, called J2, translates a flattened shape, like a rugby ball, and as the orders go up, 3, 4... the external figure is more and more complex. However, it is important to realize that this is a pragmatic representation, as the physical reality is more complex. Such series of parameters, the gravitational moments, will inform us one by one, about the equilibrium figure of the external surface of the envelope of the studied body.
Several attempts have been made over the past centuries to calculate these gravitational moments, whether in the case of the earth (and yes, the earth is not spherical !), rocky planets or stars. Physicists of the past centuries have enjoyed searching for analytical forms, i.e., more or less complex formulas elaborated from the knowledge of the physical properties of the body (mass, density, ...) and of its rotation speed, allowing « in fine » to perform the calculation. This is possible for a body of uniform density in constant rotation. Newton, in 1867, was the first to establish a simple but approximate formula, taken up again by Huygens in 1690 in a form still valid today. In 1743, Clairaut, a French physicist, tackled the problem again and gave an elegant formulation, still in the case of a body rotating at constant speed, but of variable density ρ(r). The idea at the time was to find the best equilibrium figure for the Earth's external surface, especially since the theory could be compared with observations. Clairaut will be followed by many others, such as Bruns in 1878, who introduced the concept of « Figure of a rotating body », then Radeau in 1885, Wavre in 1932, Molodensky in 1945 or Moritz in 1990, to name only a few, and who all refined the models.
In the case of rocky planets, the theory, completed by results deduced from dedicated satellites, has become very robust and allows to obtain extremely precise values of successive gravitational moments. For example, for Mars, J2 is 0.001860718 (from a model developed with 73 terms (!), as described by Yuan in 2002). For Ceres, a small planet orbiting in our solar system, J2 is 0.03240, J4 is -0, 00237 and J6, 0.00237, allowing in turn to get an idea of the internal composition of the star, as described by Rambeaux in 2015.
The problem is more difficult in the case of a star because it is a fluid body. Chandrasekhar (American astronomer of Indian origin, Nobel Prize winner in 1983) developed in 1933 a very complete theory, but solely in the case of a uniform rotation. The theory was then considerably improved, notably by Maeder, in 1999, who gave a more general formulation. The underlying physics is very complex because the rotation influences the stellar evolution and the transport of chemical elements inside the star can take place. So how do these different effects shape the observed surface? What is it in the case of the Sun, a non-homogeneous star from the center to the surface (almost all the mass is concentrated in a layer occupying the first internal quarter), in non-uniform rotation, both from the center to the surface, but also from the equator to the poles ?
For a very long time, the Jn and J2 at first, have not aroused much interest because of two significant facts : first, their orders of magnitude are very low. On the other hand, they cannot be measured directly, models are required, and thus the values will be dependent on the model adopted. On the first point, based on a very large number of results, Pireaux & Rozelot in 2003, were able to assign to J2 a value of about 0.2 parts per million [i.e. (2.0 ± 0.4) ×10-7], now commonly accepted. On the second point, several indirect observations have been proposed, the results supporting the above value. As J2 is directly related to the flattening, it follows that the polar diameter of the Sun is shorter by about 12 km than the equatorial diameter, for an average diameter of some 1 391 000 km (so a flatness of ∼ 8.6 parts per million !). The higher order gravitational moments are even weaker and are, for the moment at least, not considered (and their order of magnitude poorly defined).
One may wonder the interest of running behind a value that is close to zero... At least for three reasons. The first is to give the most precise values possible of the parameters that characterize a star, including the sun. This is what is called astrometry, a science in full force at the beginning of the last century, still relevant today when it comes to describe finely the properties of a celestial body. For example, the flatness of stars. The measurements are still very difficult because at the limit of detection of instruments. However, the identity cards of the Sun, the planets, the stars, must be provided and satisfactory.
The second is that in some celestial mechanics formulas, gravitational moments must be taken into account. In our solar system, the orbits of the planets share a common plane within a few degrees. This coplanarity was inherited from a protoplanetary disk (already discovered by Laplace in 1796) and has been maintained throughout the 4.5 billion years of history of our solar system... The precise calculation of the inclination of the orbits considers the gravitational moments. The same is true for extrasolar planetary systems which also form in thin disks (but we do not know what proportion of these systems keep their primordial coplanarity throughout their life). Except for limited special cases, mutual inclinations are generally difficult to measure. In systems already known to possess multiple transiting planets, the inclinations tend to be small, on the order of ∼ 1 - 2◦, increasing when they are closest to the star. A mechanism for misalignment was proposed by Spalding in 2020, which involves the gravitational moment of the rapidly rotating host star.
The third reason calls for the precise determination of ephemeris, i.e., the prediction of the position of the stars in the sky over time. Celestial and nautical almanacs are thus elaborated by three independent institutes, one in Russia (EPM in Saint Petersburg), another in the USA (JPL, in Pasadena) and the last one in Paris (IMCCE). These ephemerides are computed from more and more precise observations (Laser-moon, radar observations of planets, satellite tracking, very long baseline interferometry...) and which allow to obtain, for example in the case of our solar system, positions of planets within a few meters! The determination of these orbits uses gravitational moments, which can be deduced from space measurements by a process of successive adjustment of the data to the results. This process is a bit complicated but gives good results, for example in the case of the space probe Messenger mission, orbiting Mercury, the method gives for the Sun, J2 0.2246 parts per million [J2 = (2.246 ± 0.022) × 10-7]. The high precision obtained allows to go back to the general relativity (GR) parameters proving its universality (in other words, alternative theories to GR are unlikely).
This article is innovative in several respects. First, it reaffirms the nominal value of the fist solar gravitational moment, J2, which would be 0.207 parts per million [J2 = (2.07 ± 0.03) × 10-7]. Such a faint order of magnitude could be considered as void, but J2 is important, lying at the crossroad of astrometry, celestial mechanics, and General Relativity. Even if it is very exaggerated, but to give an idea of what has been highlighted, the solar surface is far from being perfectly spherical and looks more like a « cantaloup » melon with asperities variable over time... The amplitude modulation varies on a periodic time scale of about 90 years. Such results help to explain that the values found at different times, from observations, may differ somewhat. Moreover, the authors show for the first time that J2 is negatively correlated with the solar cycle when the latter is in its maximum period of activity, and vice versa (stronger correlation with the cycle in minimum period). This mechanism could take place in a solar subsurface layer called leptocline (from Greek leptos, thin), highlighted by the author in 2001 and validated by two American authors, Kitashvili and Kosovichev in a 3-dimensional model in 2022. Such an original result can be later incorporated in theories aiming at better understanding the functioning of the solar machine with time. It is thus a nice advance in the solar physics field.
Référence
Exploring the Temporal Variation of the Solar Quadrupole Moment J2, Astrophysical Journal (ApJ - AAS41872).
Contacts
Saliha Eren, The Arctic University of Norway, Department of Physics and Technology, Postboks, saliha.eren@uit.no
Jean-Pierre Rozelot (OCA-retired), jean-pierre.rozelot@grenoble-inp.org






